Deriving a Computational Model¶

We will do a time-step approximation of the movement of the nodes, based on spring and electrostatic forces. We will assume that the graph has no self-loops.

A Motivation In Graph Theory¶

Definition 1 Given a set $\mathcal{W}$, a graph $G$ is a proper subset of the Cartesian product, $\mathcal{W}\times \mathcal{W}$, such that for any $(A,B)\in G$, it is true that $A\neq B$ and $(B,A)\in G$.

Example 2
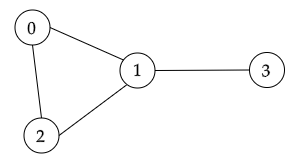
Let $\mathcal{W}=\{0,1,2,3\}$. Then $$G=\{(0,1),(1,0),(0,2),(2,0),(1,2),(2,1),(1,3),(3,1)\} \subset \mathcal{W}\times \mathcal{W}$$ is a graph. Since the standard notation for $G$ is redudent, we will remove every symmetric element: $$G=\{(0,1),(0,2),(1,2),(1,3)\}.$$

We can have a visual representation of graphs in the plane by drawing labeled vertices and connecting them according to the connections in the graph.

Example 2 (continued)
The graph $G$ can be drawn in the plane as

However, (very frustratingly) $G$ can also be drawn as

.

which is obviously not ideal.

Definition 3 A graph is planar if it can be plotted in the plane with no intersecting edges.

Note that many planar graphs can be plotted with interesecting edges, and unfortunately, not every graph is planar.

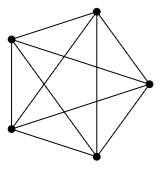
Example 4
The $K_5$ graph is not planar:

There is no way to rearrange the nodes in the $K_5$ so that no two edges cross.

There are some necessary Planarity Tests:

Euler's Formula
The Four Color Theorem
$K_5$ and $K_{3,3}$ as subgraphs

Nothing about a graph definition (a set of tuples) defines how to plot the nodes of a graph, so we might consider asking is: How can we efficiently plot graphs in a visually satisfactory way? If A graph is planar, how can we plot it to reflect that structure? If a graph is not planar, what is the most flattering way we can play the nodes? We will assume that the graph has no self-connecting nodes, since if it does, it will not change how we should place nodes.

Intuitive Behavior¶

One intuitive path to take, is to use physicial phenomenon to move the nodes into an optimal place.

Recall some governing force equations that will be useful:

Spring Force $$F_s=kx$$
Electrostatic Force $$F_e=Q\frac{q_1q_2}{r^2}$$

The nodes can be modeled as charged particles, and the connections as springs. In this sense, starting from random positions the nodes will have the freedom to equalize and spread out, but be constrained by the edge connections.

Here is the general idea:

So how should we define $q$ and $m$? Intuitively, we want the vertices to be more "free" the less connected they are, and when a node is very connected, we want it to have more inertia. Luckily, there is already convemtional notation for this!

Definition 5 The degree of node $A$ in a graph $G$ is the number of nodes that are connected to $A$, and is notated $\text{deg}(A)$.

Moving the Nodes with Newton's 2nd Law¶

In order to translate forces ot movement, we need Newton's Second Law.

Let $\Delta t$ be the time step of the simulation. For each node $A$, we can use the net force on $A$ to approximate its displacement, $\Delta \vec{d}$:

\begin{align*} & \sum \vec{F}(A)=m\vec{a}= \operatorname{deg}(A) \frac{d^2}{dt^{2}} \vec{d}\\ \implies & \frac{\sum\vec{F}(A)}{\operatorname{deg}(A)} =\frac{d^2}{dt^{2}} \vec{d}\approx \frac{\Delta \vec{d}}{\Delta t^2}\\ \implies & \Delta \vec{d}\approx \frac{\Delta t^2}{\deg(A)}\sum\vec{F}(A). \end{align*}

Finding the Net Force on a Node¶

In order to use Newton's Second Law, we need to find $\sum \vec{F}$, the net force on node $A$.

For each node $A$, define

$\mathcal{X}$: the set of nodes in the graph that are not equal to $A$;
$\mathcal{Y}$: be the set of nodes connected to $A$.

Then for each $B$ in $\mathcal{X}$, and $C$ in $\mathcal{Y}$, \begin{align*} \vec{F}_e(A,B) & =Q\frac{\deg(A)\deg(B)}{\|\vec{AB}\|^2}\frac{\vec{AB}}{\|\vec{AB}\|},\text{ and}\\ \vec{F}_s(A,C) & =k(\|\vec{AC}\|-\ell)\frac{\vec{A C}}{\|\vec{A C}\|}, \end{align*}

where $\ell>0$ is the unstretched spring length; $Q<0$ and $k>0$ are the electric field, and spring constants, respectively. Then $$\sum\vec{F}(A)=\vec{F}_g(A)+\sum_{B\in\mathcal{X}}\vec{F}_e(A,B)+\sum_{C\in \mathcal{Y}}\vec{F}_s(A,C).$$

The Master Equation¶

We can now define precisely the change made to each node during each time step.

\begin{align*} \sum\vec{F}(A) & = \sum_{B\in\mathcal{X}}\vec{F}_e(A,B)+\sum_{C\in \mathcal{Y}}\vec{F}_s(A,C) = \sum_{B\in\mathcal{X}}Q\frac{\deg(A)\deg(B)}{\|\vec{AB}\|^2}\frac{\vec{AB}}{\|\vec{AB}\|}+\sum_{C\in \mathcal{Y}}k(\|\vec{AC}\|-\ell)\frac{\vec{A C}}{\|\vec{A C}\|},\\ \end{align*}

which implies that $$\Delta \vec{d} \approx \Delta t^2\left( Q\sum_{B\in\mathcal{X}}\left(\frac{\deg(B)}{\|\vec{AB}\|^2}\frac{\vec{AB}}{\|\vec{AB}\|}\right)+k\sum_{C\in \mathcal{Y}}\left(\frac{(\|\vec{AC}\|-\ell)\vec{A C}}{\deg(A)\|\vec{A C}\|}\right)\right).$$

We will let $\ell = 1$.