$\newcommand{\M}{M_{n\times n}\Z_2} \newcommand{\Mas}{\mathcal{M}} \newcommand{\Z}{\mathbb{Z}} \newcommand{\N}{\mathbb{N}} \newcommand{\Nn}{\N_n\times\N_n} \newcommand{\CL}{\operatorname{CL}} \newcommand{\c}[1]{ \textbf{#1}} \newcommand{\ker}{\text{ker}} \newcommand{\col}{\text{col}}$
Algebra in the Game Lights Out¶
Table of contents¶
- Game Background
- Mathematical Structure and Questions
- $D_4$ acts on $\M$
- Classifying $S_n$, the set of solvable boards
- The Group $\Lambda_n$
- Chasing Lights
Game Background¶
The classic version of Lights Out was an electronic handheld puzzle released by Tiger Electronics in 1995, and is played on a $5\times 5$ keypad of square buttons that are either lit or dark. The object is to turn all of the lights off by clicking the buttons on the board, and the one rule is deceptively simple: clicking a button changes its own state, as well as the state of the 4 directly adjacent buttons, if they exist (clicking on an corner only changes the state of 3 buttons and clicking an edge button not in a corner changes the state of 4 buttons). Below is some sample game play from Wikipedia):
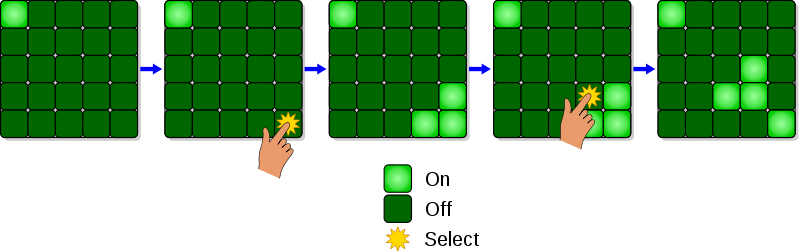
You can play online at GeoGebra.
Mathematical Structure and Questions¶
We will generalize to $n\times n$ boards, which can be viewed as the matrices in the abelian group $\M$. The group operation is matrix addition $\bmod 2$, where zeros represent a dark square and a 1 represents a lit square. Naturally, $0\in\M$ is the empty (or dark) board. Note that this representation is intuitive and consistent with an exclusive-or "XOR" action on boards: each board is it's own inverse!
We will label each button as an ordered pair of positive integers at most $n$, so if we let $\N_n$ denote the set $\{1,\dots,n\}$, then $\Nn$ is the complete set of buttons in the game.
1. $D_4$ Acts on $\M$¶
If $X \in \M$ is a solvable board, then so is any rotation or reflection of $X$. Hence, if we are interested in finding the number of solvable boards, one might choose only to count solutions up to this symmetry. Clearly, $D_4$ gives a group action $(\cdot)$ on $\M$. We can use Burnside's Lemma to count the number of possible board states up to rotation and reflection.
- If $n$ is even, any $n\times n$ board is comprised of concentric squares of $4(n-1), 4(n-3), \dots, 4(3), 4(1)$ buttons.
- The identity transformation fixes $2^{n^2}$ boards.
- There are two rotations by $\pi/2$ in $D_4$, and each of these rotations fixes $2^{(n-1)+(n-3)+\dots+(3)+(1)}=2^{\left(\frac{n}{2}\right)^2}$ boards. This equality holds since the sum of the first $k$ odd integers is $k^2$.
- There is one rotation by $\pi$ in $D_4$, which fixes $2^{\frac{n^2}{2}}$ boards.
- There is one reflection across the board horizontally and one vertically, each of which fixes $2^{\frac{n^2}{2}}$ boards.
- There are two reflections across the board diagonally, each of which fixes $2^{1+2+\dots+n}=2^{\frac{n(n+1)}{2}}$ boards.
- If $n$ is odd, any $n\times n$ board is comprised of concentric squares of $4(n-1), 4(n-3), \dots, 4(4), 4(2), 1$ buttons.
- The identity transformation fixes $2^{n^2}$ boards.
- There are two rotations by $\pi/2$ in $D_4$, and each of these rotations fixes $2^{(n-1)+(n-3)+\dots+(4)+(2)+1}=2^{a\left(\frac{n+1}{2}\right)}$ boards, where $a(n)=n^2-n+1$ is the $n$-th central polygonal number (
A002061). Indeed this equality holds: do an induction on odd $n\in\N$. The base case of $n=1$ holds since $$1=1^2-1+1=a(1)=a\left(\frac{1+1}{2}\right).$$ Now choose any odd $k\in\N$ and suppose that $(k-1)+(k-3)+\dots+(4)+(2)+1=a\left(\frac{k+1}{2}\right)$. Then
\begin{align*} ((k+2)-1)+((k+2)-3)+\dots+(4)+(2)+1 & = (k+1)+(k-1)+(k-3)+\dots+(4)+(2)+1 \\& = (k+1)+a\left(\frac{k+1}{2}\right) \\& = (k+1)+\left(\frac{k+1}{2}\right)^2-\left(\frac{k+1}{2}\right)+1 \\& = \frac{x^2}{4}+x+\frac{7}{4} \\& = \left(\frac{k+3}{2}\right)^2-\left(\frac{k+3}{2}\right)+1 \\ & = a\left(\frac{k+3}{2}\right) \\ & = a\left(\frac{(k+2)+1}{2}\right).\end{align*} - There is one rotation by $\pi$, which fixes $2^{n\left(\frac{n-1}{2}\right)+\left(\frac{n-1}{2}\right)+1}=2^{(n+1)\left(\frac{n-1}{2}\right)+1}$ boards.
- There is one reflection across the board horizontally and one vertically, each of which fixes $2^{\frac{n(n+1)}{2}}$ boards.
- There are two reflections across the board diagonally, each of which fixes $2^{1+2+\dots+n}=2^{\frac{n(n+1)}{2}}$ boards.
Then, using Burnside's Lemma, there are \begin{align*} N(n)=&\begin{cases} \frac{1}{2^{n^2}}\left(2^{n^2}+2\cdot2^{\left(\frac{n}{2}\right)^2} + 2^{\frac{n^2}{2}} + 2\cdot2^{\frac{n^2}{2}} + 2\cdot2^{\frac{n(n+1)}{2}} \right) & n\equiv 0\bmod 2\\ \frac{1}{2^{n^2}}\left(2^{n^2} + 2\cdot 2^{\left(\frac{n+1}{2}\right)^2-\left(\frac{n+1}{2}\right)+1} + 2^{(n+1)\left(\frac{n-1}{2}\right)+1} + 2\cdot 2^{\frac{n(n+1)}{2}} + 2\cdot 2^{\frac{n(n+1)}{2}} \right) & n\equiv 1\bmod 2 \end{cases}\\ =&\begin{cases} 2^{n^{2}-3}+2^{\frac{n^{2}-8}{4}}+2^{\frac{n^{2}-6}{2}}+2^{\frac{n^{2}-4}{2}}+2^{\left(\frac{n(n+1)-4}{2}\right)} & n\equiv 0\bmod 2\\ 2^{n^{2}-3}+2^{\frac{n^{2}-5}{4}}+2^{\frac{n^{2}-5}{2}}+2^{\frac{n^{2}+n-2}{2}} & n\equiv 1\bmod 2 \end{cases} \end{align*} $n\times n$ board states up to rotation and reflection.
def N(n):
if n % 2 == 0:
return 2**(n**2-3)+2**((n**2-8)/4)+2**((n**2-6)/2)+2**((n**2-4)/2)+2**((n**2+n-4)/2)
return 2**(n**2-3)+2**((n**2-5)/4)+2**((n**2-5)/2)+2**((n**2+n-2)/2)
Here is a table sumerizing the first few values of $N(n)$:
table(rows=[(n,N(n)) for n in range(1,7)], header_row=["$n$", "$N(n)$"])
This sequence appers in OEIS here: A054247.
EXAMPLE
Let's look at the $2\times 2$ case. The orbits of $D_4$ on $M_{2\times2}\Z_2$ are
This list is consistent since $N(2)=6$.
2. Classifying $S_n$, the set of solvable boards¶
Write $C_{i,j}\in\M$ for the "click" matrix that is the result of clicking the empty board on square $(i,j)\in\Nn$. Note that the resulting board from clicking a board $b$ on square $(i,j)$ is $b + C_{i,j}$ and that this clicking addition is commutative!
For any solvable board $b$, by definition, there exists a set $\Theta\subseteq\Nn$ of buttons for which $$b + \sum_{(i,j)\in\Theta}C_{i,j}=0.$$ Since the addition of these click matrices is commutative, to solve the board, we can press the buttons in $\Theta$ in any order we wish. Note, however, that nothing about this construction guarantees that $\Theta$ is unique: indeed, it possible that a board has two distinct sets of buttons that can be pressed in order to solve it.
At this point, it is clear that the set of solvable boards is $$S_n=\left\langle C_{i,j}\mid (i,j)\in\Nn\right\rangle,$$ the subgroup of $\M$ generated by all possible click matrices.
Write $\hat{b}\in\Z_2^{|b|^2}$ for the vector formed by appending the successive rows of $b$.
EXAMPLE
If $$b=C_{1, 1}=\begin{pmatrix}1 & 1 & 0\\ 1 & 0 & 0\\ 0 & 0 & 0\end{pmatrix},$$ then $$\hat{b}=\hat{C}_{1, 1}=(1,1,0,1,0,0,0,0,0)^T.$$
Let $$\Mas_n=\begin{pmatrix}\hat{C}_{1,1} & \dots & \hat{C}_{1,n} & \hat{C}_{2,1} & \dots & \hat{C}_{2,n} & \cdots & \hat{C}_{n,1} & \dots & \hat{C}_{n,n}\end{pmatrix}$$ denote the master click matrix for size $n\times n$ boards.
import numpy as np
from IPython.display import *
_C = lambda n : [1] * n**2
_R = lambda n : ([0] + [1] * (n - 1)) * n
_L = lambda n : _R(n)[::-1]
_U = lambda n : [1] * (n * (n - 1)) + [0] * n
_D = lambda n : _U(n)[::-1]
def Mas(n):
m = np.zeros((n**2, n**2), dtype=np.int)
C, R, L, U, D = _C(n), _R(n), _L(n), _U(n), _D(n)
for i in range(n**2):
m[i][i] = C[i]
m[i][(i - 1) % n**2] += R[i]
m[i][(i + 1) % n**2] += L[i]
m[i][(i + n) % n**2] += U[i]
m[i][(i - n) % n**2] += D[i]
return m
For example,
display(Markdown("$$\Mas_3 = " + latex(Matrix(Mas(3))) + " $$"))
Notice that $\hat{w}=\Mas_nv$, where $$w=\sum_{v_{in+j}=1} C_{i,j}.$$ In other words, the vector $v$, whose entries are 0 or 1, selects certain columns of $\Mas_n$ (click matrices) to sum. This means that $$\text{col}(\Mas_n)=S_n,$$ and that in order to solve a board $b$, one need only find $v$ so that $\Mas_nv=b$.
The following are all equivalent:
- every $n\times n$ board is solvable
- $|S_n|=2^{n^2}$
- $\Mas_n$ is full rank (has a rank deficiency of 0)
- $\Mas_nv=0$ has a unique solution
- $\det(\Mas_n)\neq 0$
and the following OEIS sequences record some related results:
A075462$n\to$ number of solutions to $\Mas_nv=0$A076436$n$ for which $\Mas_nv=0$ has a unique solutionA117870$n$ for which $\Mas_nv=0$ does not have a unique solution. Also is the sequence of numbers $n$ such that an $n\times n$ parity pattern exists (seeA118141)A159257$n\to$ rank deficiency of $\Mas_n$A296350$n$ for which $\det(\Mas_n)\neq 0$
Slightly related:
A075463$n\to$ number of solutions to $\Mas_nv=0$, where $v$ is counted distinct up to rotation and reflectionA076437$n$ for which $\Mas_nv=0$ has a unique solutions up to rotation and reflection
Hunziker, Machiavelo, and Park prove in [4] that the rank deficiency of $\Mas_n$ is the degree of $$\gcd(f_n(x),\ f_n(x+1)),$$ where $f_n(x)=U_n(x/2)$ over the field $\Z_2$ and $U_n$ is the $n$-th Chebyshev Polynimial of the second kind.
NOTE
Chebyshev Polynomials are of "two kinds", $T_n$, the first (discussed in [5]), and $U_n$ the second (discussed in [6]). They are defined to satisfy $$\cos(n\theta)=T_n(\cos\theta)\ \ \ \text{and} \ \ \ \sin(n\theta)=U_{n-1}(\cos\theta)\sin\theta.$$ $T_n$ and $U_n$ also have recursive defintions: $$T_n(x)=\begin{cases}1 & n = 0\\ x & n = 1\\ 2xT_{n-1}(x)-T_{n-2}(x)& \text{otherwise};\end{cases}$$ and $$U_n(x)=\begin{cases}1 & n = 0\\ 2x & n = 1\\ 2xU_{n-1}(x)-U_{n-2}(x)& \text{otherwise}.\end{cases}$$
The result above implies that the values of $n$ for which every $n\times n$ board is solvable are those for which $$\deg\left(\gcd(f_n(x),\ f_n(x+1))\right) = 0,$$ or equivelantly, $f_n(x)$ and $f_n(x+1)$ are relatively prime.
We can use Sage to generate the polynomials $f_n(x)$ and $f_n(x+1)$ as well as find the degree of their gcd.
F = GF(2)['x']
x = var('x')
f = lambda n, z: F(chebyshev_U(n, z/2))
def row(n):
f_x = f(n,x)
f_x_1 = f(n,x+1)
g = f_x_1.gcd(f_x)
d = g.degree()
return (n, f_x, f_x_1, g, d)
table(rows=[row(n) for n in range(15)],
header_row=["n", "$f_n(x)$", "$f_n(x+1)$", "$\gcd(f_n(x), f_n(x+1))$", "$\deg$"])
EXAMPLE
If we are interested in finding the rank deficiency of $\Mas_6$, the master click matrix for a $6\times 6$ lights out board, first compute \begin{align*} U_2(x) & = 2x(U_1(x))-U_0(x)=2x(2x)-1=4x^2-1\\ U_3(x) & = 2x(U_2(x))-U_1(x)=2x(4x^2-1) - 2x = 8x^3-4x\\ U_4(x) & = 2x(U_3(x))-U_2(x)=2x(8x^3-4x)-4x^2-1 = 16x^4 - 12x^2 + 1\\ U_5(x) & = 2x(U_4(x))-U_3(x)=2x(16x^4 - 12x^2 + 1)-8x^3-4x=32x^5 - 32x^3 + 6x\\ U_6(x) & = 2x(U_5(x))-U_4(x)=2x(32x^5 - 32x^3 + 6x)-16x^4 - 12x^2 + 1=64x^6 - 80x^4 + 24x^2 - 1\\ \end{align*} so \begin{align*}f_6(x)&=U_6(x/2)\\&=64(x/2)^6 - 80(x/2)^4 + 24(x/2)^2 - 1\\ &= x^6 - 5x^4 + 6x^2 - 1\\ &\equiv x^6 + x^4 + 1.\end{align*} Then \begin{align*}f_6(x+1)&=(x+1)^6+(x+1)^4+1\\&=x^6 + 6x^5 + 16x^4 + 24x^3 + 21x^2 + 10x + 3\\ &\equiv x^6 + x^2 + 1\end{align*} so $$\dim(\ker(\Mas_6))=\deg(\gcd(x^6 + x^2 + 1, x^6 + x^4 + 1))=\deg(1)=0.$$ This is what we expect, sinceA159257$(6)=0$; indeed, every $6\times 6$ lights out board has a solution.
When $\Mas_n$ is not full rank, we can generate the set of solvable boards by finding $\col(\Mas_n)$. In doing this effiently, we will find a basis of columns of $\Mas_n$.
It is proven in [1] (as well as many other places including by Sutner in 1989) that it is always possible to turn a blank board all on; this is known as the "all-ones problem". Since the diagonal of $\Mas_n$ is all ones, the proof is simply an application of the more general result that the diagonal of any symmetric and binary matrix is contained in its column space.
Conjecture 2.1 If $\ell$ columns of $\Mas_n$ are linearly independent, then the first $\ell$ are linearly independent.
Question 2.2 Is there a way to simply charactarize $\gcd(f_n(x),f_n(x+1))$?
Question 2.3 It is interesting to note it seems as though $\dim(\ker(\Mas_n))\neq 0\implies\dim(\ker(\Mas_{2n+1}))\neq 0$. The same pattern is seen in the columns of Neller's Pictures of effects patterns. Are (and if so, how are) these related?
Question 2.4 Since there is some nonzero term in the symmetric matrix $\Mas_n$, Theorem 1 in [2] tells us that when $\Mas_n$ is invertible (i.e. every board is solvable) there exist some square binary matrix $X$ such that $X^TX=\Mas_n$. What does this say about $\Mas_n$?
Question 2.5. Is there a way to more simply determine $S_n$? In other words, is there a method of determining if an element of $\M$ is in $S_n$ by observation, possibly by determining some invarient? There are some sufficient conditions given by Jaap.
Question 2.6. When $\Mas_n$ is full rank, how can we categorize it as an element of the general linear group?
3. The group $\Lambda_n$¶
$S_n$ is normal since $\M$ is abelian, so we can consider the quotient group $$\Lambda_n=\M/S_n,$$ and define an equivalence relation $\lambda$ on $\M$ so that two boards are related if and only if they are in the same coset of $S_n$. This relation corresponds to being able to click buttons on one board to arrive at the other since \begin{align*} b_1\sim_\lambda b_2 &\iff b_1+S_n=b_2+S_n\\ & \iff (b_1+S_n)-(b_2+S_n)=S_n\\ & \iff b_1-b_2\in S_n\\ & \iff b_1-b_2=\sum_{(i,j)\in\Theta}C_{i,j}\ \ \ \text{for some }\Theta\in\Nn\\ & \iff b_1+\sum_{(i,j)\in\Theta}C_{i,j}=b_2. \end{align*}
This is interesting because this suggests there are more specific classifications than just "solvable" and "unsolvable": some unsolvable boards might not be reachable from other unsolvable boards!
Note that the size of $\Lambda_n$ gives a measure of how solvable $\M$ is as a whole: if $|\Lambda_n|$ is small, there are few cosets of $S_n$, so $|S_n|$ is relatively large in $\M$. Otherwise, $|\Lambda_n|$ is large, so there are many cosets of $S_n$, and the number of solvable boards is small in $\M$.
Recall that in the previous section we found that $S_n=\col(\Mas_n)$. Since $\Mas_n$ is a $n^2\times n^2$ matrix with nullity $\deg\left(\gcd(f_n(x),\ f_n(x+1))\right)$, the rank plus nullity theorem tells us that $$\dim(\col(\Mas_n)) = n^2 - \deg\left(\gcd(f_n(x),\ f_n(x+1))\right).$$ Since the weight on a column of $\Mas_n$ is either a 1 or 0, $$|\col(\Mas_n)|=2^{n^2-\deg\left(\gcd(f_n(x),\ f_n(x+1))\right)}.$$ Then we can write $$|\Lambda_n|=\frac{|\M|}{|\col(\Mas_n)|}=\frac{2^{n^2}}{2^{n^2-\deg\left(\gcd(f_n(x),\ f_n(x+1))\right)}} = 2^{\deg\left(\gcd(f_n(x),\ f_n(x+1))\right)}=2^{\dim(\ker(\Mas_n))}=|\ker(\Mas_n)|.$$
This means that $|\Lambda_n|=$A075462$(n)$ is also the number of boards in the nullspace of $\Mas_n$. In other words, $|\Lambda_n|$ is the number ways you can click an empty board and attain an empty board.
Here are the first few values of $|\Lambda_n|$:
size_of_Lambda = lambda n: 2**(f(n,x).gcd(f(n,x+1)).degree())
table(columns=[(n,size_of_Lambda(n)) for n in range(1,20)], header_column=["$n$", "$|\Lambda_n|$"])
In 2, we discussed that every empty board can be clicked to be full, and it turns out that $|\Lambda_n|=|\ker(\Mas_n)|$ is also the number of ways to do so! This is because since $1\in\col(\Mas_n)$, there is a $v_0\in\Z_2^{n^2}$ for which $\Mas_nv_0=1$, and the set of vectors $v$ for which $\Mas_nv=1$ is $v_0+\ker(\Mas_n)$.
Question 3.1 How do elements of $\ker(\Mas_n)$ correspond to cosets of $S_n$?
Question 3.2. What is a charactarization of $\Lambda_n$?
Question 3.3. What is a simple set of representatives for $\Lambda$?
4. Chasing Lights¶
Similarly to the "click" matrix defined above, let $E_{i,j}$ denote the board with only the square $(i,j)$ lit. Define $$L_n=\left\langle E_{n,i}\mid i\in\N_n\right\rangle\leq\M,$$ the subgroup of $\M$ generated by boards with lights on only in the bottom row. It is clear that $L_n\cong\Z_2^n$.
The chasing lights algorithm is a function $$\CL:\M\to L_n.$$
To perform it, iterate through each button in the first $n-1$ rows, starting in the top left corner and processing horizontally. If the button is lit, click the button directly below it. This process will result in a board with lights on only in the the $n$th row. $\CL$ is clearly surjective, but not injective.
Chasing lights is interesting and useful because it gives an upperbound on $|\Lambda|$: every board in $\M$ is equivalent under $\lambda$ to (in the same coset of $S_n$ as) some board in $L$, which has size $2^n$, so there are at most $2^n$ cosets of $S_n$.
Now define a surjective group homomorphism \begin{align*} g:L_n & \to \Lambda_n\\ b & \mapsto b+S, \end{align*} and notice that $$\ker(g)=\{x\in L_n\mid g(x)=S_n\}=\{x\in L_n\mid x\in S_n\}=L_n\cap S_n,$$ so by the First Isomorphism Thereorem, $$\Lambda_n\cong L_n/\ker(g)=L_n/(L_n\cap S_n).$$
This means that the dimmension of $\Lambda$ is at most $n$, for if $L_n\cap S=\{0\}$, then $\Lambda\cong L_n$, which has dimmension $n$. In the "best case senario", $L_n\cap S=L_n$ (since $L_n\subseteq S$), so all boards are solvable and $\Lambda\cong L_n/L_n\cong\{0\}$ has dimmension 0.
It turns out that we can use Chasing Lights to give an even simpler categorization of the $n\in\N$ for which every $n\times n$ board is solvable (Some of the following analysis is from [7].
Note that $\CL(C_{i, j}) = 0$ if $i > 1$ since the chasing lights algorithm would just click $(i, j)$ to make the board dark. So, $$\CL(S_n) = \CL(\langle C_{1, j}\mid j\in\N_n\rangle).$$ Thus, if $b$ is a solvable board, then there is a set of indices $J\subseteq \N_n$ such that $$\CL(b) = \CL\left(\sum_{j \in J} C_{1, j}\right).$$ This means $$\CL\left(\CL(b) + \sum_{j \in J} C_{1, j}\right) = 0,$$ so if you can figure out what $J$ is, then you know which buttons to click in the top row so that doing $\CL$ again results in a dark board.
You can figure out what $J$ is as follows. Let's view $\CL$ as a function from the set of all boards to $L_n$, and let's view the elements of $L_n$ as column vectors. So, $\CL(b)$ is the column vector that is the transpose of the bottom row of the board after doing the $\CL$ algorithm on $b$.
We just proved the following:
Let $K_n$ be the $n\times n$ matrix whose $j$th column is $\CL(C_{1, j})$. For any board $b$, $b$ is solvable if and only if $K_nv = \CL(b)$ has a solution, and $J$ above is just the set of indices corresponding to the nonzero elements of $v$. All boards are solvable if and only if $K_n$ has full rank.
The transposes of these $K_n$ matrices are depicted in Neller's Pictures of effects patterns.
import numpy as np
from IPython.display import *
class Board(object):
""" board with 0-based indexing """
def __init__(self, n):
self.board = np.zeros((n,n), dtype=int)
self.n = n
def find_first_light(self):
for i in range(self.n):
for j in range(self.n):
if self.board[i][j] == 1:
return (i, j)
return (self.n,self.n)
def click(self, i, j):
self.board[i][j] = 1 - self.board[i][j]
if j - 1 >= 0:
self.board[i][j - 1] = 1 - self.board[i][j - 1]
if j + 1 < self.n:
self.board[i][j + 1] = 1 - self.board[i][j + 1]
if i + 1 < self.n:
self.board[i + 1][j] = 1 - self.board[i + 1][j]
if i - 1 >= 0:
self.board[i - 1][j] = 1 - self.board[i - 1][j]
def chase_lights(self):
first = self.find_first_light()
while first[0] < self.n - 1:
self.click(first[0] + 1, first[1])
first = self.find_first_light()
def __repr__(self):
return str(self.board)
def K(n):
K_matrix = np.zeros((n,n), dtype=int)
for j in range(n):
b = Board(n)
b.click(0,j)
b.chase_lights()
K_matrix[j] = b.board[n-1]
return K_matrix.T
We can use sage to generate these $K_n$ matrices. Here is an example:
display(Markdown("$$K_5 = " + latex(Matrix(K(5))) + " $$"))
We can also show that $\CL$ is a homomorphism.
Proof. [7]
For any board X, define the height of $X$ to be the smallest nonnegative integer $k$ such that $X$ is dark in the first $n - k$ rows. So, for example: the dark board has height zero; a board in $L_n$ has height 1; a board with a light on on the top row has height $n$; a board whose first row is dark and whose second row has a light on has height $n - 1$. Let’s prove that $$\CL(X+Y)=\CL(X)+\CL(Y).$$ by induction on the height of $X$ and $Y$. The base case is when $X$ and $Y$ have height at most $1$. Then $\CL(X) = X$, $\CL(Y) = Y$, and $\CL(X + Y) = X + Y$ so the theorem clearly holds in this case. Next, fix $1 < k \leq n$ and suppose the equation is true for all $X$, $Y$ of height at most $k - 1$. Let $X$ and $Y$ be boards of height at most $k$. Theere are sets of indices $A$, $B$ (possibly empty) such that \begin{align*} X' & = X + \sum_{j\in A} C_{k-1,j} \\ \CL(X) & = \CL(X') \\ Y' & = Y + \sum_{j\in B} C_{k-1,j} \\ \CL(Y) & = \CL(Y') \\ \end{align*} and $X'$, $Y'$ have height at most $k-1$. Thus \begin{align*} \CL(X)+\CL(Y) & = \CL(X') + \CL(Y') \\ & = \CL(X' + Y') &&\text{[by the inductive hypothesis]}\\ & = \CL\left(X+Y+\sum_{j\in A\cup B}C_{k-1,j}\right). \end{align*} Since $X + Y$ has height at most $k$ (as does $X + Y + C$ where $C$ is any sum of clicks on row $k - 1$), it sufices to prove: if $B$ is a board of height $t$, then $\CL(B + C_{t-1,j}) = \CL(B)$ for any $j$. This is obviously true if $B_{t,j} = 1$ because then $C_{t−1,j}$ is part of the chasing lights algorithm. If $B_{t,j} = 0$, then when you apply the $\CL$ algorithm to $B + C_{t−1,j}$ you could for the first step click $(t − 1, j)$, and again we have $\CL(B +C_{t−1,j}) = \CL(B)$.
References¶
[1] https://www.win.tue.nl/~aeb/ca/madness/madrect.html
[2] https://www.researchgate.net/publication/257334572_Proving_properties_of_matrices_over_Z2
[3] https://mathworld.wolfram.com/LightsOutPuzzle.html
[4] https://reader.elsevier.com/reader/sd/pii/S0304397504001823?token=B8AFDD138A41FFA8A32AE25E5CCF801E54CC3F069A1349841FCC6F91AE5EF87997540C953BECAE8415651995B25A96D6
[5] https://mathworld.wolfram.com/ChebyshevPolynomialoftheFirstKind.html
[6] https://mathworld.wolfram.com/ChebyshevPolynomialoftheSecondKind.html
[7] Keir Lockeridge, Personal communication
